Portfolio diversification based on price movements
- Melvin

- May 15, 2022
- 6 min read
Updated: May 17, 2022
[You can download the Diversification (Price Correlation) Excel from the Resources page]
In a previous post, I provided some background on how you may want to approach this mysterious thing called "diversification". It's necessary to understand what it is and how to approach it, but to be honest I'm not a fan of how subjective it all is. In this post, we take a more numerical approach.
As mentioned previously, what we want to avoid is for everything to go down at the same time, which severely limits our options. We know that some products tend to move less than others (e.g. blue-chip stocks vs growth stocks), some tend to move in opposite directions (e.g. stocks vs bonds), some are DESIGNED to move in opposite directions (e.g. STI ETF vs an Inverse ETF like SSS.SI), and some aren't correlated with each other at all (e.g. stocks vs cash). Most stocks that we're interested in are tied to the economy in the sense that they tend to do very well when the economy's fine. Chances are, the average investor's portfolio will mainly comprise of these stocks. More experienced investors will mix in some utility or defense-related stocks (stocks that traditionally tend to be a good hedge against economic downturns). However, as we've seen oh-so-recently, when the market capitulates even these "recession-proof" stocks get hit hard. So what can you do? Have too little of these "safe" stocks and your portfolio won't be spared the bloodbath. Have too much of them (and/or cash) and the portfolio will be too slow-growing (not to mention boring. Imagine having to balance out every dollar you invest in, say, TSLA with 9 dollars in Singapore Savings Bonds). How do you balance the ups and downs in an efficient manner?
The first thing to do is to characterize the products you're holding and/or interested in. In this example, I took the historical price data from 1 Apr 2022 to 1 May 2022 for the top 5 constituents in the STI (DBS, OCBC, UOB, Singtel, Jardine) which account for over 50% weightage in the index. I also look at Capitaland China Trust and Manulife US REIT, 2 Real Estate Investment Trusts based in 2 very different countries. Finally, I also look at an STI ETF (ES3.SI), A35.SI which is a bond ETF (so that we can compare stocks vs bonds), and an inverse ETF (SSS.SI). I used my stock price scavenger (which you can download from the Resources page) to download the prices, and copy-paste them into the Input section of the Price Correlation Excel.
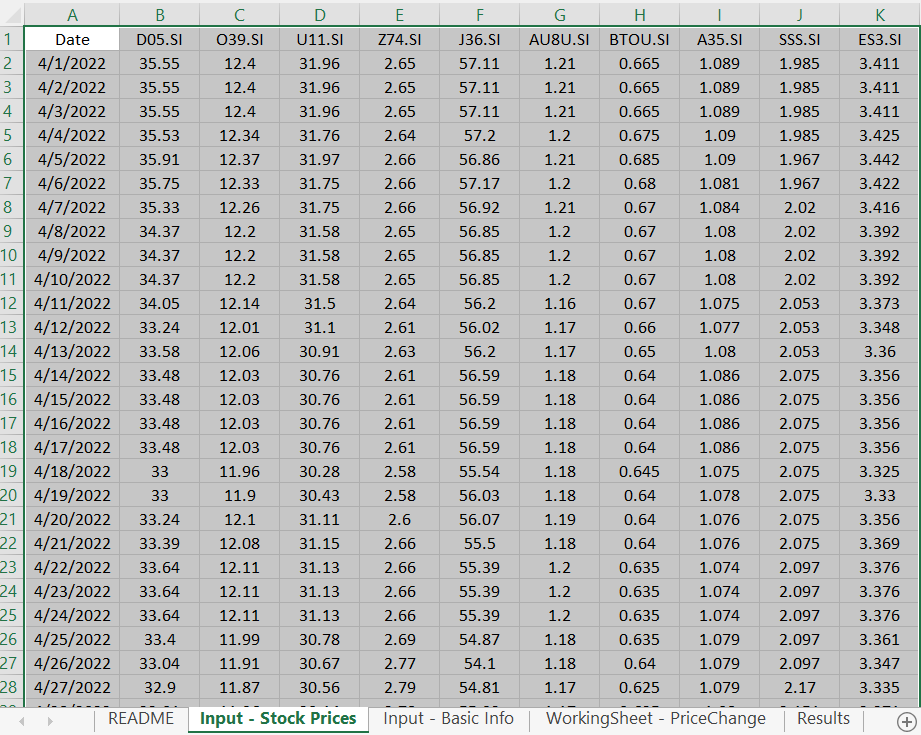
Next, I entered details of my holdings in the 'Input - Basic Info' worksheet. I assume I purchased about 10k worth of each of those first 6 stocks.

That's it! We're now ready to analyze the results.
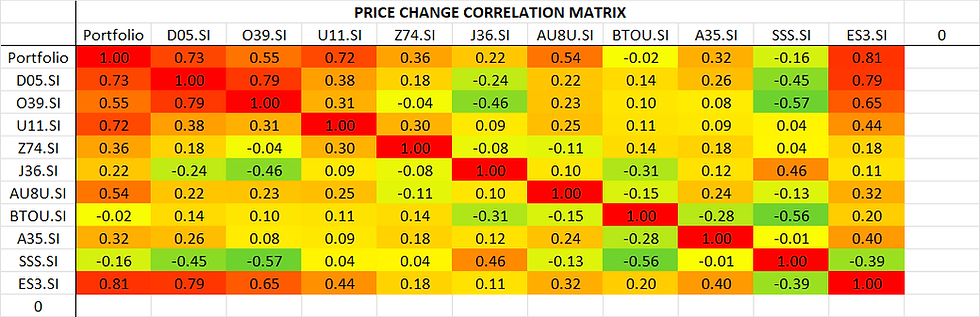
As you may have suspected, having the top 5 constituents of the STI make up 80% of our portfolio will make us track the index quite closely, and sure enough the portfolio and the index (ES3.SI) have a correlation coefficient of 0.81. Now let's say you've heard about the US-China conflict and the lockdowns in China, and think "hey perhaps getting a REIT in the US will balance out my China REIT!". Well, the 2 tickers we're looking at (AU8U vs BTOU) have a correlation of -0.15, which I'll leave to you to decide if you want to consider that inversely-correlated (i.e. they'll "balance" each other out) or uncorrelated (i.e. they'll just do their own thing). Now, if you want to get something to "balance out" the whole portfolio, SSS.SI has the lowest correlation with the portfolio at -0.16, which sorta makes sense since our portfolio tends to track the STI quite closely, and SSS.SI is designed to move opposite the index (I'm not sure it's doing a very good job though, given that its correlation with ES3.SI is only -0.39). If you want to remove a stock from the portfolio without "losing diversification", you could consider D05.SI or O39.SI, both of which are strongly correlated with each other which hint that they may be "duplicates". To decide, we see that they're both weakly correlated with U11.SI, so it's a tie here. Now, D05.SI's correlation with Z74.SI and J36.SI are 0.18 and -0.24 respectively, while O39.SI's correlation with those are -0.04 and -0.46. We now see that removing D05.SI makes sense if our aim is to keep the portfolio's constituent price changes as inversely-correlated as possible so that they balance each other out. Sure enough, when we sell all our holdings in D05.SI (i.e. set D05.SI Holdings in 'Input - Basic Info' to 0), we get the following results:
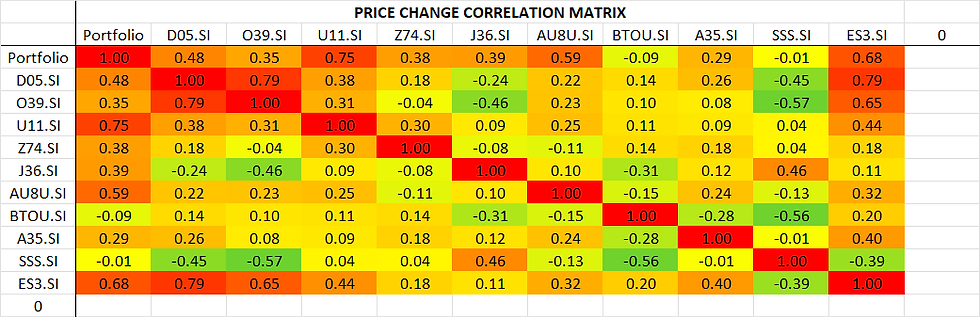
We see that the portfolio became more strongly correlated with the remaining tickers, which makes sense. If you only had 1 stock, your portfolio will have a correlation of 1.00 with that stock! What we want, is to decrease the correlation our portfolio has with any/all of the components. Previously, the portfolio has a correlation of 0.73 with D05.SI, which means it'll be quite affected by D05.SI's price movements. Now, the portfolio has a correlation of 0.75 with U11.SI, which means it'll be even more affected by U11.SI's price movements. Are we less diversified than before? Well, it's the less of 6 evils I suppose; as long as you don't have 2 tickers that are perfectly correlated with each other it's hard to choose something to sell without losing some diversification. I could sell O39.SI instead, which will make the resulting portfolio have a maximum correlation coefficient of 0.71 (with U11.SI), but at the cost of making it much more strongly correlated with every stock in the portfolio.
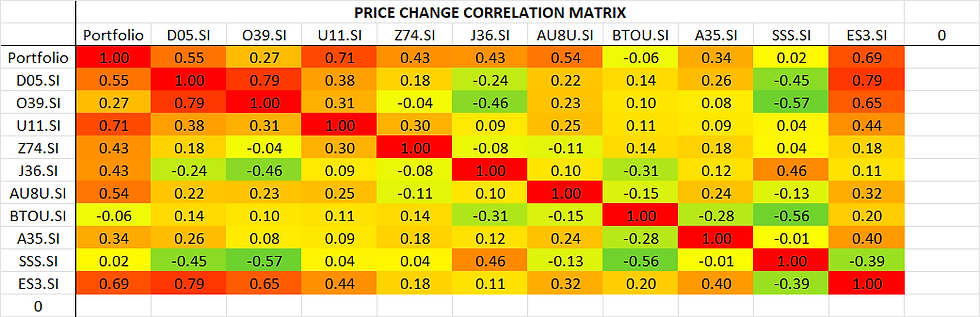
In the end, it once again goes back to what you're trying to achieve. If you're trying to make your portfolio a Zen haven such that no matter what any of the constituent stock prices are doing, other constituents' price changes will balance it out, you will want to keep the coefficients as low as possible for ALL the constituents. If you want to make sure you're not overly affected if one of the constituents crash, you will want to reduce the maximum coefficient.
We now come to the crux of the problem: You want to add more stocks to your portfolio to diversify. However, adding multiple stocks that are strongly correlated with each other doesn't help. As you add more stocks, it gets more and more difficult to find new stocks that aren't strongly correlated with what you already have. In fact, this is the problem with many active investors: as they start to add more stocks to their portfolio, their portfolio starts to track the index more closely. At some point, they'll start wondering why they bother picking stocks instead of simply buying the index components. Personally, I just impose a limit such that the portfolio doesn't have a coefficient of more than, say, 0.8 with any individual component. I also like to have the ES3.SI data there as a reference, so that I can aim for a higher correlation with it when markets are good (so that I fly with the benchmark index) and a low coefficient when I sense something amiss and want to adopt a risk-off stance.
If you've made it this far, congratulations! But there are always caveats. First, the correlation coefficients are calculated from the Stock Price input data. As with any analysis that looks at time data, you must be very careful when selecting the time period. If you use data from a period where the markets are in panic-mode and there's indiscriminate selling, chances are that everything will be more correlated than they're supposed to be, since there's downward pressure on everything regardless of geography or sector or instrument-type. If you use data from period that's just entering a typical recession, you will see strong inverse correlation between "safe-haven stocks" and "high-risk stocks". If you use data from a bull market you'll once again see strong correlation market-wide, as the indiscriminate buying pushes all prices up. Ideally you'll want your data period to include all of that, but companies change. A small investment startup could be inversely correlated to many of your stocks 10 years ago, but as they grew and expanded they could end up strongly correlated to some of the big names in your portfolio as they acquired large stakes in them. If you used data across the entire period you would end up with some sort of average, which isn't exactly reflective. Ideally you'd find the largest period possible where the company's profile is reflective of its situation today, but this is easier said than done, since companies are usually constantly changing.
Another major point to note, and perhaps the most important thing here, is that we're only looking at price correlation here. It does not give us any insight into the fundamentals of the company. You could pick companies A and B because they're inversely correlated over the past few months (because A kept rising and B kept falling). You buy the stocks and 2 months later a recession hits, and the price of A starts falling, and the price of B... keeps falling. Looking at price correlation only tells us how the prices moved relative to each other in the time period for which you fed it data, nothing more, nothing less. This of course also brings us to the oft-quoted disclaimer: past performance does not guarantee future results.
I'll end this post here as it has gone on long enough. This price correlation Excel can help you to quantify how the prices of your holdings tend to move relative to one another. Combine this, with the previous post about fundamentals, and you'll have a decent picture of what diversification can mean (emphasis on can, since, as we've seen, while the overarching idea is the same, the way you apply it will depend greatly on your situation and what you want to do with it). Have fun!


Comments